Causal Budget Framework
Queue → GR (1-PN) demo

Queue → GR (1-PN) — How it works

This demo builds \( \alpha(r) \) and \( \psi(r) \) from queues, maps them to a refractive index \( n(r)=\psi/\alpha \), then shows that photon bending and 1-PN orbital precession match textbook GR after a live, per-run normalization.

Ray bending ≈ \(4GM/(bc^2)\) Line integral agrees Orbit precession ≈ \(6\pi GM/[a(1-e^2)c^2]\)

1) Queue buffering → \( \alpha(r), \psi(r), n(r) \)

We integrate two queues along radius, a time-queue \(b_t\) and a space-queue \(b_s\), using a simple source–drain law:

\( \displaystyle \frac{db}{dr} = S(r) - \kappa\,b, \qquad S(r)\propto \frac{GM}{r^2 c^2} \)

Then we map queues to the isotropic-form lapse and scale:

\( \displaystyle \alpha(r) = \frac{1-\tfrac12 b_t}{1+\tfrac12 b_t}, \qquad \psi(r) = \bigl(1+\tfrac12 b_s\bigr)^2, \qquad n(r)=\psi/\alpha. \)
Build queue fields on a radial grid

2) Self-calibration: no magic constants

The queue ODE gives the right shape but not the absolute gradient scale. Each run we measure the uncalibrated straight-line deflection and match it to the analytic GR result \( \delta\theta_{\rm GR}=4GM/(bc^2) \). That produces a live factor \(k_{\rm eff}\) used everywhere.

Per-run normalization

This is a per-run normalization, derived from the current sliders. Nothing is hardcoded.

3) Photon bending via Fermat

We propagate the ray’s direction \(\hat{\mathbf{k}}\) with the transverse gradient of \(n(r)\):

\( \displaystyle \mathbf{k}' = \frac{\nabla n - (\hat{\mathbf{k}}\!\cdot\!\nabla n)\,\hat{\mathbf{k}}}{n} \)
Ray tracing with calibrated gradients

4) Orbit precession (1-PN reference)

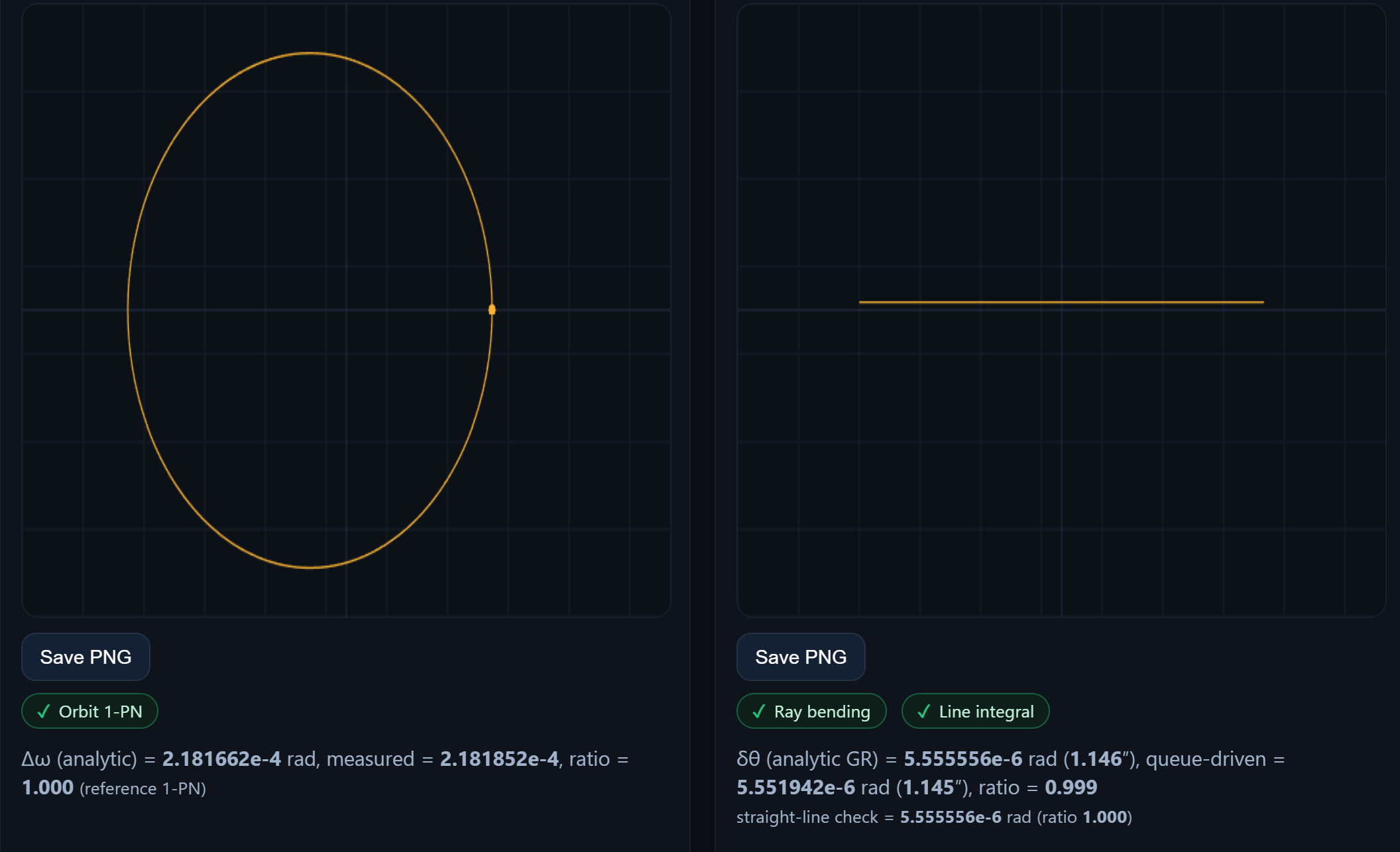
The orbit panel is a GR 1-PN reference using the Binet equation for \(u(\phi)=1/r\), integrated with RK4. Perihelia are found by true local minima refined by a quadratic fit, then a regression over all perihelia estimates the per-orbit precession.

Binet + perihelion refinement

What to look for

  • Metrics panel: toggle “magnify \( \alpha,\psi \)”. The queue curves overlap the exact isotropic reference after calibration.
  • Photon panel: enable “magnify view” to see the tiny bend. The chip turns green when the measured deflection matches \(4GM/(bc^2)\).
  • Orbit panel: the orange dots mark refined perihelia. The chip compares measured precession to \(6\pi GM/[a(1-e^2)c^2]\).
  • Presets: defaults show a generic case, “Mercury-like” tightens steps for a clean precession measurement.
No hidden constants

The only normalization is computed live each run by matching the straight-line integral to the analytic GR angle. Change any slider and it recalibrates.