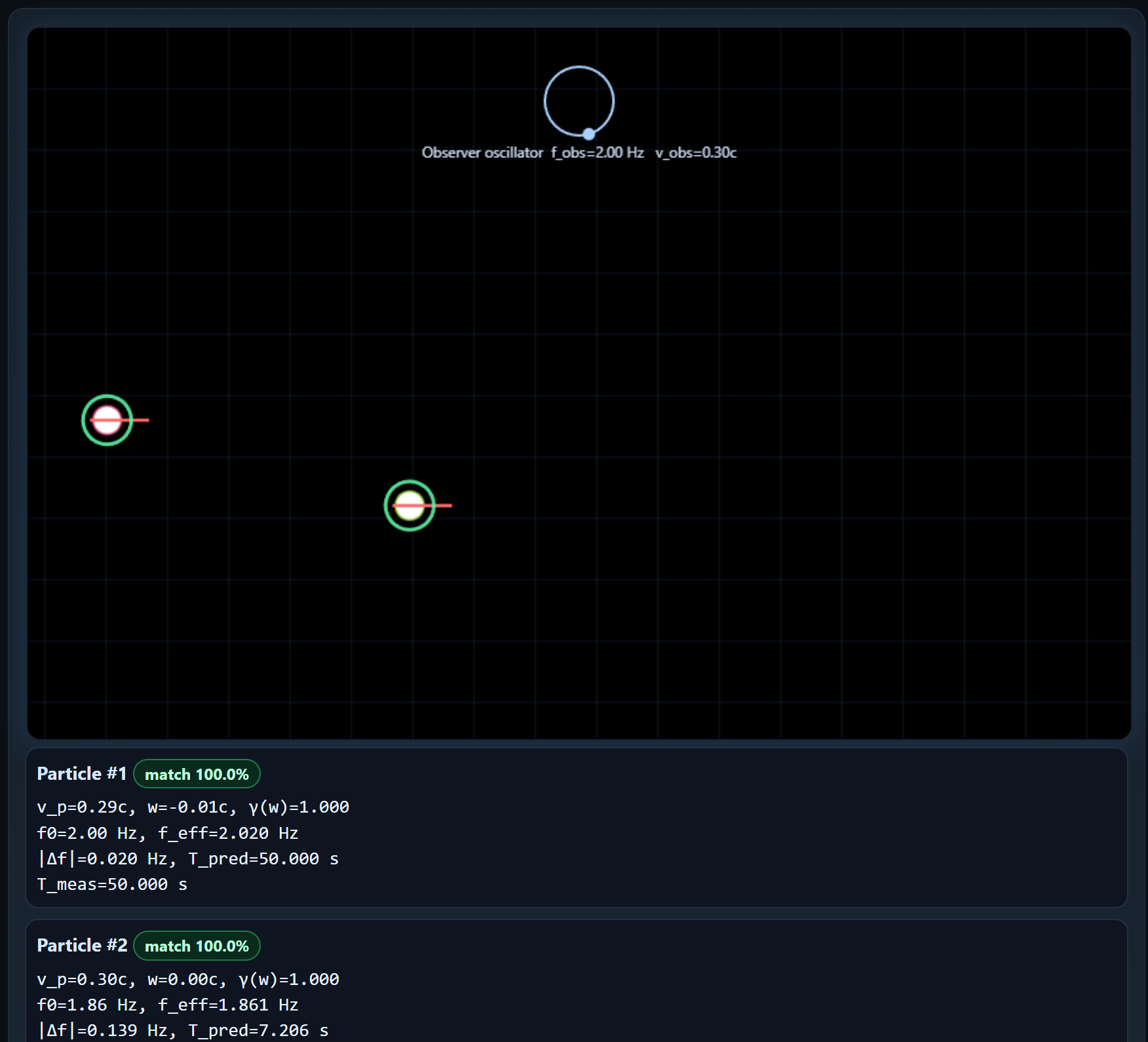
Beat-Matching with the Observer
This demo compares **clock rates** seen by an observer using two rules: SR (symmetric), where the clock rate is \( \mathrm{d}\tau/\mathrm{d}t = \sqrt{1-w^2} \), and CBF (directional), where the rate is \( \mathrm{d}\tau/\mathrm{d}t = \max(0.01,\;1 + v_\text{obs} - v_p) \). Each particle’s oscillation is beat-matched against the observer’s oscillator. A green flash marks each phase alignment event, and cards report the **predicted** beat period \(T_\text{pred}=1/|f_\text{eff}-f_\text{obs}|\) versus the **measured** period from those events.
Top: observer oscillator. Center: moving particles with color intensity indicating clock rate. Right: live cards with \( \gamma(w) \), \( f_\text{eff} \), and beat statistics.
How this maps to CBF
In CBF, every entity shares a per-tick budget \( C = T + M \). Motion uses T, internal ticking uses M. Relative motion, fields, or pacing shift that split, changing the **effective tick rate** an observer infers. Beat-matching is the Event Ledger’s **temporal gate** in miniature: it detects when two oscillators align well enough to register a commit. The demo visualizes that gate by comparing the observer’s oscillator against each particle’s effective frequency derived from the chosen rule (SR or CBF). Where alignment happens frequently, the measured beat period matches \( 1/|f_\text{eff} - f_\text{obs}| \) and the card shows a high match.
What to expect
- SR mode: The clock rate depends only on the SR relative velocity \( w=(v_p-v_\text{obs})/(1-v_p v_\text{obs}) \). Increase \( |w| \) to slow the particle’s clock and widen \( |f_\text{eff}-f_\text{obs}| \), which shortens \( T_\text{pred} \).
- CBF mode: Clock rate tilts directionally with \( 1 + v_\text{obs} - v_p \). Particles moving with the observer tick faster, those moving against tick slower, producing asymmetric beat behavior when you flip directions.
- Beats are exact: The detector uses integer-turn phase crossings, so measured periods should closely match \( 1/|Δf| \) even at low frame rates.
Settings
| Control | Default | Effect |
|---|---|---|
| Observer speed \(v_\text{obs}\) | 0.30 c | Shifts relative velocity \(w\). In CBF mode, also changes the directional clock factor. |
| Observer frequency \(f_\text{obs}\) | 2.0 Hz | Sets the observer’s oscillator. Changing this alters \( Δf \) and thus \( T_\text{pred} \). |
| Particle speed (new) | 0.60 c | Each particle stores its own speed. Affects \(w\) and the particle clock rate. |
| Particle rest frequency \(f_0\) (new) | 2.0 Hz | Base oscillator for each particle. Effective frequency is \( f_\text{eff}=f_0\cdot\mathrm{rate} \). |
| Clock rule | CBF (directional) | Toggle between SR’s symmetric rate and CBF’s directional rate to compare predictions. |
| Scene speed | 420 px/s | Visual only, makes motion across the canvas easier to see. |
Key Code
The demo exposes both rules. SR uses Einstein addition for the relative speed \(w\). CBF uses a directional pacing rule relative to the observer. Either way, the particle’s effective frequency is \(f_\text{eff} = f_0 \cdot \mathrm{rate}\).
To avoid missed beats when the phase jumps over zero between frames, the detector counts integer turns of the **unwrapped** relative phase and linearly interpolates the exact crossing time inside the frame. This makes \(T_\text{meas}\) track \(1/|Δf|\) with high accuracy at any frame rate.
Integer-turn counting removes sensitivity to frame rate and tolerance bands. It guarantees a single, correctly timed beat per phase cycle even if multiple crossings occur inside one render step.
Illustrations


