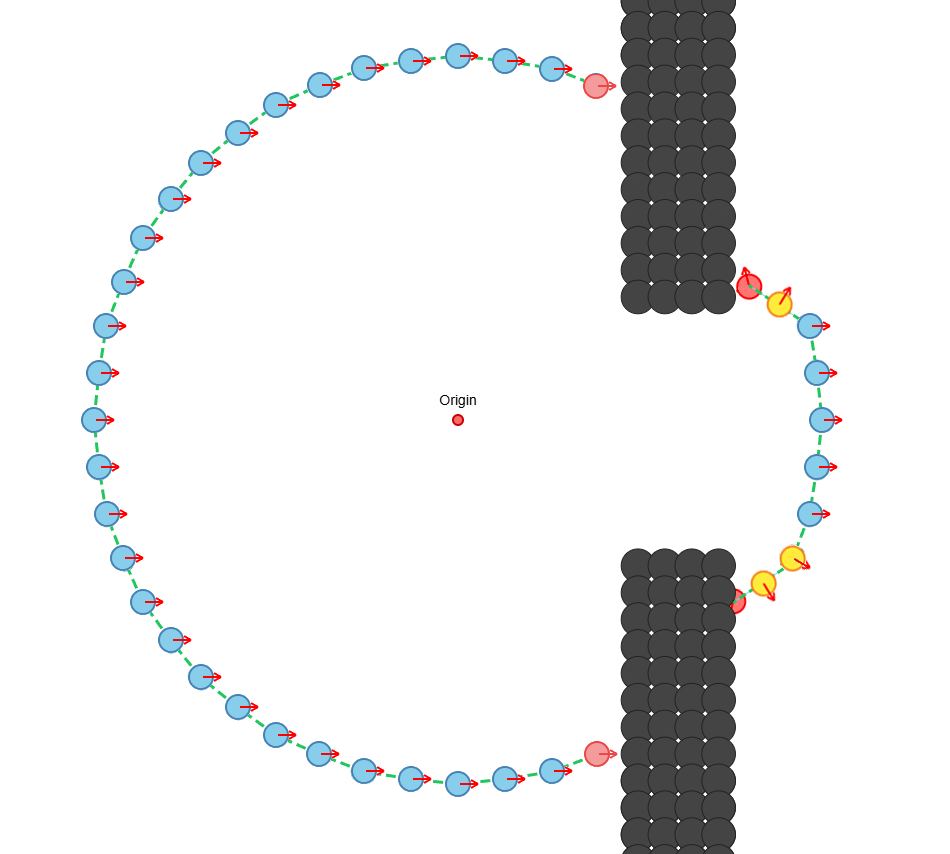
Vector CA: Diffraction and Wave Growth

This proof-of-concept demonstrates the Vector Cellular Automaton (Vector CA) model for wave propagation. In this version, each wave cell carries a direction vector, and new cells spawn outward along those directions. When the expanding wavefront encounters the wall, the vectors bend and multiply, creating a diffracted edge pattern.

The result is a “growing” wavefront that naturally rounds edges and fans into open regions—showing how diffraction can emerge directly from local vector updates without any trigonometric rules or global field solving. The pattern reproduces the same widening seen in real diffraction through slits.

The code driving this animation still has a minor angle bug in the update logic, visible as slight misalignments in some of the propagated vectors. However, the proof works: the CA successfully generates the expected curved wavefront and shows multiplication of active cells along edge boundaries.

This is the foundation for using Vector CA as a complete field model for CBF, where each wave cell evolves direction, amplitude, and phase locally, forming healing hemispheres and diffraction patterns as emergent behavior.